DuckDB 中自适应基数树的持久存储
概括:DuckDB 使用自适应基数树 (ART) 索引来强制约束和加速查询过滤。到目前为止,索引尚未持久化,导致索引信息丢失以及具有数据约束的表重新加载时间过长等问题。我们现在将 ART 索引持久化到磁盘,从而大大缩短了数据库加载时间(高达几个数量级),并且我们不再丢失现有索引的跟踪。这篇博文深入探讨了 ART 存储的实现、基准测试和未来工作。最后,为了更好地了解如何使用我们的索引,我请您回答以下调查问卷。它将指导我们定义未来的路线图。

DuckDB 使用 ART 索引来保持主键 (PK)、外键 (FK) 和唯一约束。它们还可以加速点查询、范围查询(具有高选择性)和连接。在最新版本(或 V0.4.1,取决于您阅读此帖子的时间)之前,DuckDB 不会将 ART 索引持久化到磁盘。在存储数据库文件时,只会存储有关现有 PK 和 FK 的信息,所有其他索引都是临时的,并在重新启动数据库时不存在。对于 PK 和 FK,它们会在重新加载数据库时完全重建,从而导致加载时间过长的不便。
已经发表了很多关于 ART 索引的科学著作,最值得注意的是关于同步、缓存效率和评估。但是,到目前为止,还没有关于序列化和缓冲管理 ART 树的公开作品。有人说 Tableau 中的数据库 Hyper 持久化 ART 索引,但同样,没有关于如何完成此操作的公开信息。
这篇博文将描述 DuckDB 如何存储和加载 ART 索引。特别是,如何延迟加载索引(即,仅在必要时才将 ART 节点加载到内存中)。在 ART 索引部分中,我们将介绍什么是 ART 索引、它的工作原理以及一些示例。在 DuckDB 中的 ART 部分中,我们将解释为什么我们决定在 DuckDB 中使用 ART 索引,它在哪里使用,并讨论不持久化 ART 索引的问题。在 ART 存储部分中,我们将解释如何在 DuckDB 中序列化和缓冲管理 ART 索引。在 基准测试部分中,我们将 DuckDB v0.4.0(ART 存储之前)与 DuckDB 的最新版本进行比较。我们演示了 PK 和 FK 在两个版本中的加载成本差异,以及延迟加载 ART 索引和访问完全加载的 ART 索引之间的差异。最后,在 路线图部分中,我们讨论了当前实现的缺点以及未来 ART 索引的计划列表。
ART 索引
本质上,自适应基数树是 Trie,它应用垂直和水平压缩来创建紧凑的索引结构。
Trie
Trie 是树数据结构,其中每个树级别都包含数据集的一部分信息。它们通常以字符串为例。在下图中,您可以看到包含字符串“pedro”、“paulo”和“peri”的表的 Trie 表示。根节点代表第一个字符“p”,其子节点是“a”(来自 paulo)和“e”(来自 pedro 和 peri),依此类推。
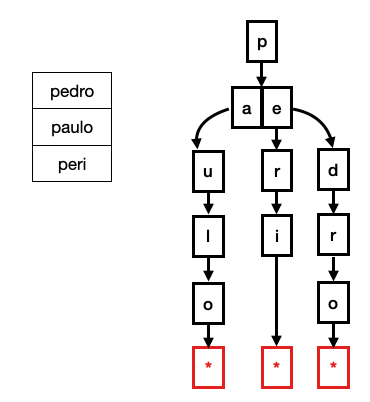
要在 Trie 上执行查找,您必须将键的每个字符与 Trie 的当前级别匹配。例如,如果您搜索 pedro,您必须检查根是否包含字母 p。如果它包含,您检查它的任何子节点是否包含字母 e,直到您到达包含指向保存该字符串的元组的指针的叶节点。(参见下图)。
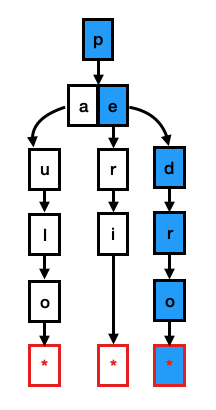
Trie 的主要优点是它们具有 O(k) 查找,这意味着在最坏的情况下,查找成本将等于字符串的长度。
实际上,Trie 也可以用于数字数据类型。但是,像字符串一样逐个字符地存储它们将是浪费的。例如,采用 UBIGINT 数据类型。实际上,UBIGINT 是一个 uint64_t,它占用 64 位(即 8 个字节)的空间。uint64_t 的最大值为 18,446,744,073,709,551,615。因此,如果像上面的示例中那样表示它,我们将需要在 Trie 上有 17 个级别。实际上,Trie 是在位扇出上创建的,它告诉每个级别的 Trie 表示多少位。一个具有 8 位扇出的 uint64_t Trie 最多有 8 个级别,每个级别代表一个字节。
为了有更现实的例子,从现在开始,这篇文章中的所有描述都将使用位表示。在 DuckDB 中,扇出始终为 8 位。但是,为了简单起见,这篇博文中的以下示例的扇出为 2 位。
在下面的示例中,我们有一个 Trie,它索引值 7、10 和 12。您还可以在它们旁边的表中看到每个值的二进制表示。每个节点由位 0 和 1 组成,旁边有一个指针。此指针可以设置为(由 * 表示)或为空(由 Ø 表示)。与我们之前的字符串 Trie 类似,Trie 的每个级别将代表两位,这些位旁边的指针指向它们的子节点。最后,叶子指向实际数据。
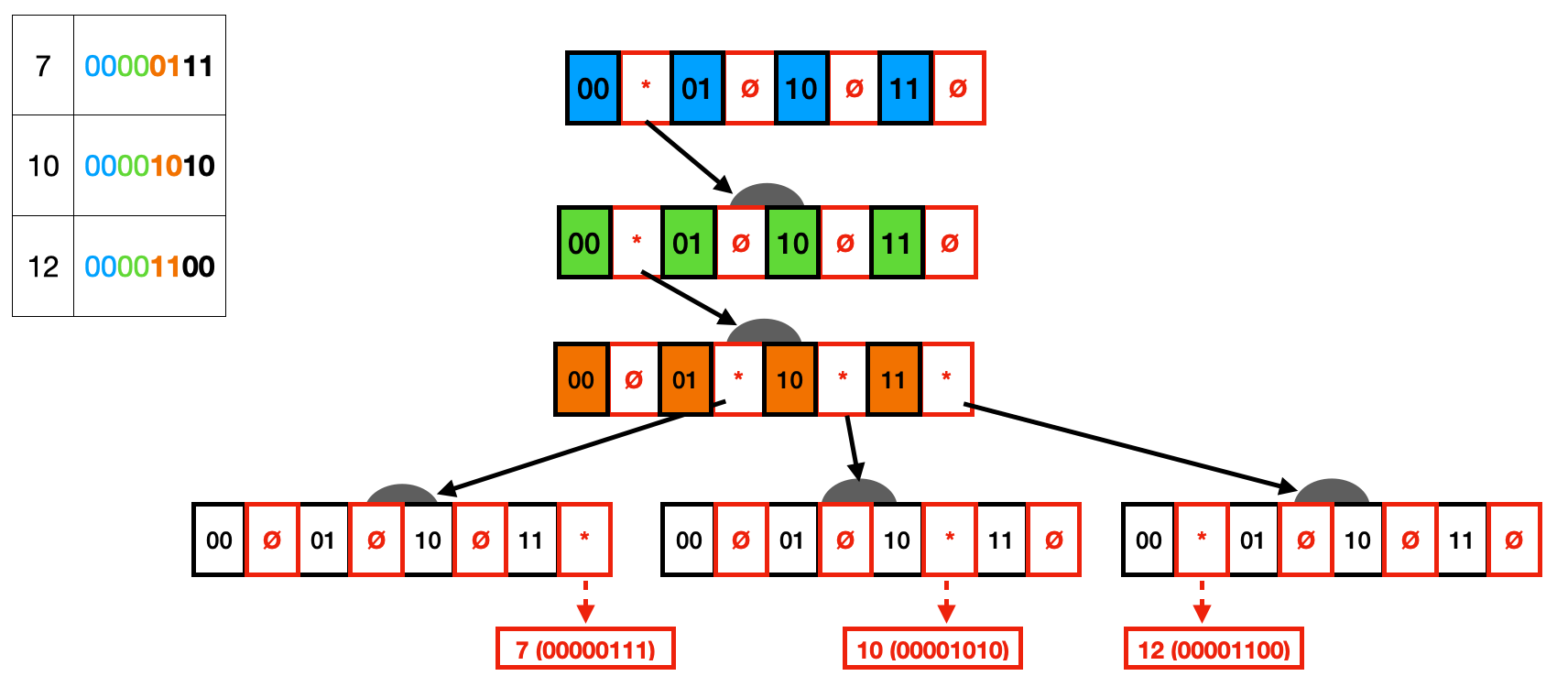
人们可以很快注意到,这种 Trie 表示在两个不同的方面是浪费的。首先,许多节点只有一个子节点(即,一条路径),可以通过垂直压缩(即基数树)来折叠。其次,许多节点具有空指针,存储空间没有任何信息,这可以通过水平压缩来解决。
垂直压缩(即 基数树)
垂直压缩的基本思想是,我们折叠只有一棵子树的节点的路径。为了支持这一点,节点存储一个前缀变量,其中包含到该节点的折叠路径。您可以在下图中看到此表示。例如,可以看出前四个节点只有一个子节点。这些节点可以作为前缀路径折叠到第三个节点(即,第一个分叉的节点)。执行查找时,键必须匹配前缀路径中包含的所有值。
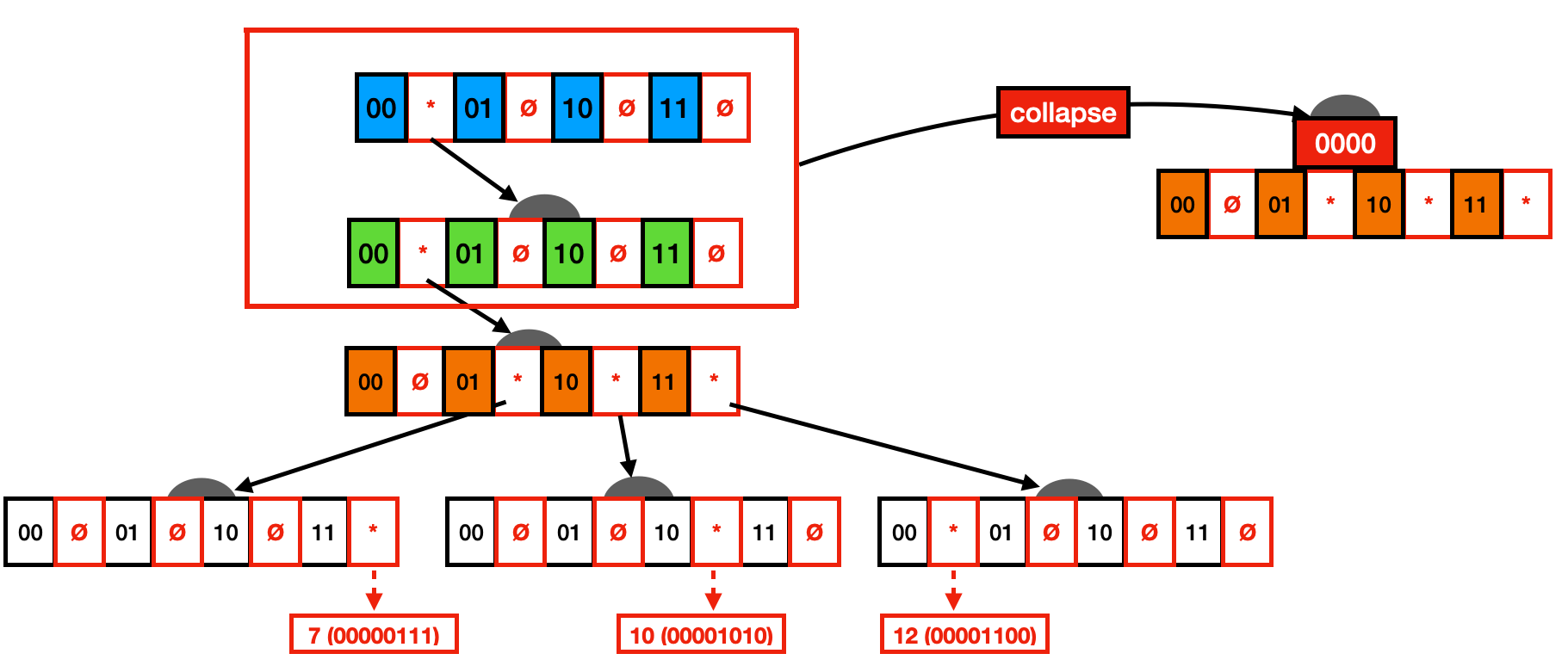
下面您可以看到垂直压缩后的 Trie。这种 Trie 变体通常被称为基数树。虽然这种 Trie 变体已经节省了大量浪费的空间,但我们仍然有许多节点具有未设置的指针。
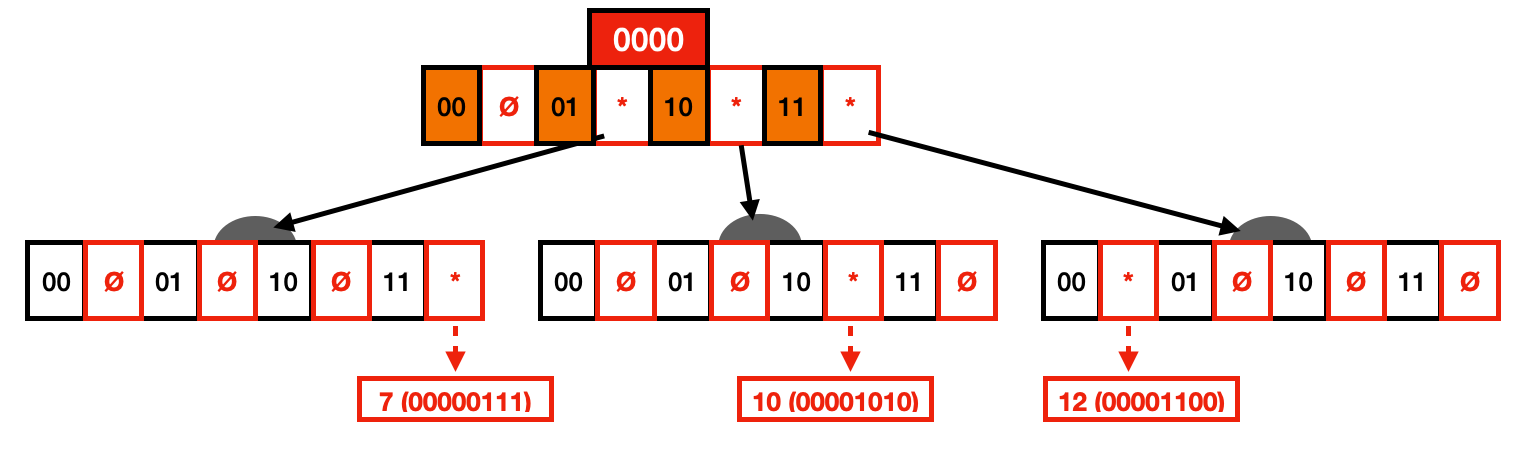
水平压缩(即 ART)
为了充分理解 ART 索引背后的设计决策,我们必须首先将 2 位扇出扩展到 8 位,这是数据库系统常见的扇出。
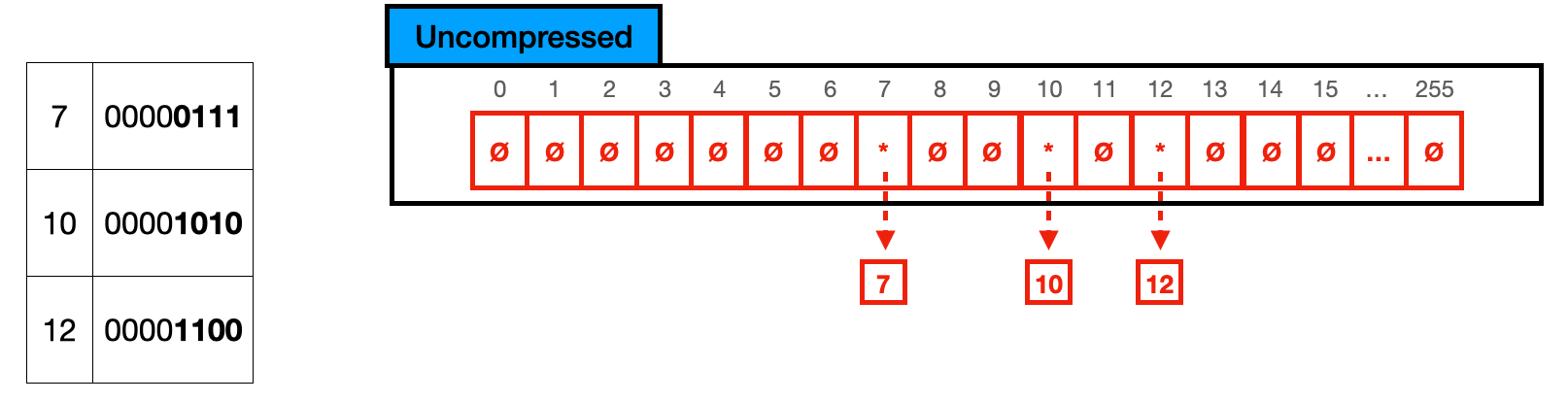
您可以在下面的 8 位 TRIE 节点中看到与之前相同的节点。实际上,这些节点将存储 (2^8) 256 个指针,键是指针的数组位置。在这种情况下,我们有一个节点,其大小为 (256 个指针 * 8 字节) 2048 字节,而实际上只利用了 24 字节(3 个指针 * 8 字节),这意味着 2016 字节完全浪费了。为了避免这种情况。ART 索引由 4 种不同的节点类型组成,这取决于当前节点的完整程度。下面我快速描述每个节点,并提供它们的图形表示。在图形表示中,我展示了节点的概念可视化,并提供了一个包含键 0、4 和 255 的示例。
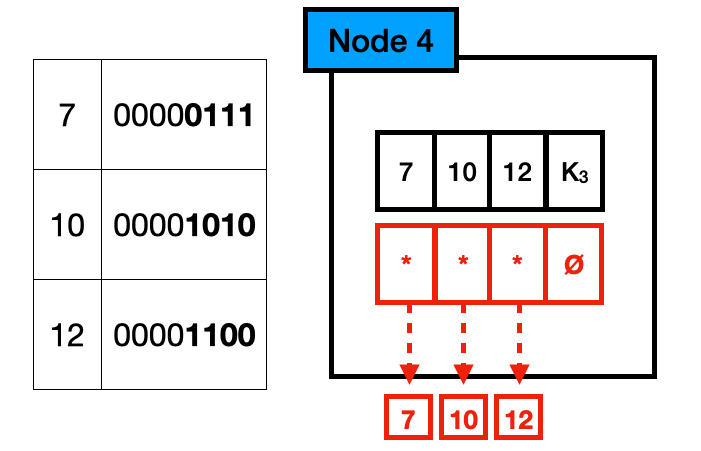
节点 4:节点 4 最多容纳 4 个不同的键。每个键都存储在一个单字节数组中,每个键有一个指针。总大小为 40 字节 (4*1 + 4*8)。请注意,指针数组与键数组对齐(例如,键 0 位于键数组的位置 0,因此其指针位于指针数组的位置 0)
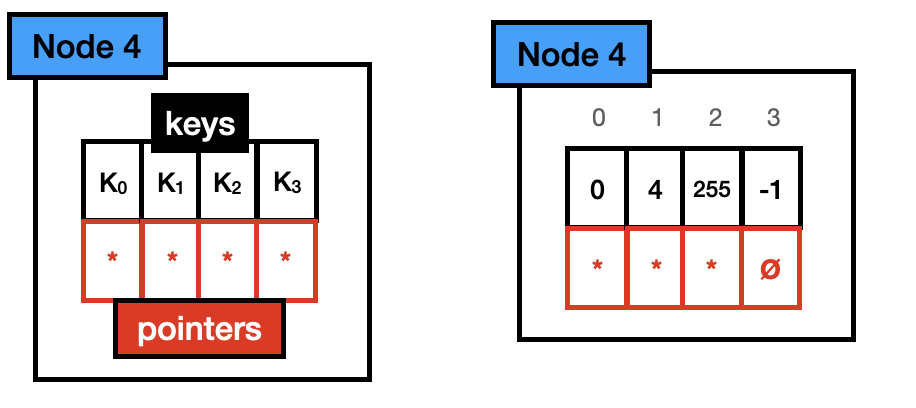
节点 16:节点 16 最多容纳 16 个不同的键。与节点 4 类似,每个键都存储在一个单字节数组中,每个键有一个指针。总大小为 144 字节 (16*1 + 16*8)。与节点 4 类似,指针数组与键数组对齐。
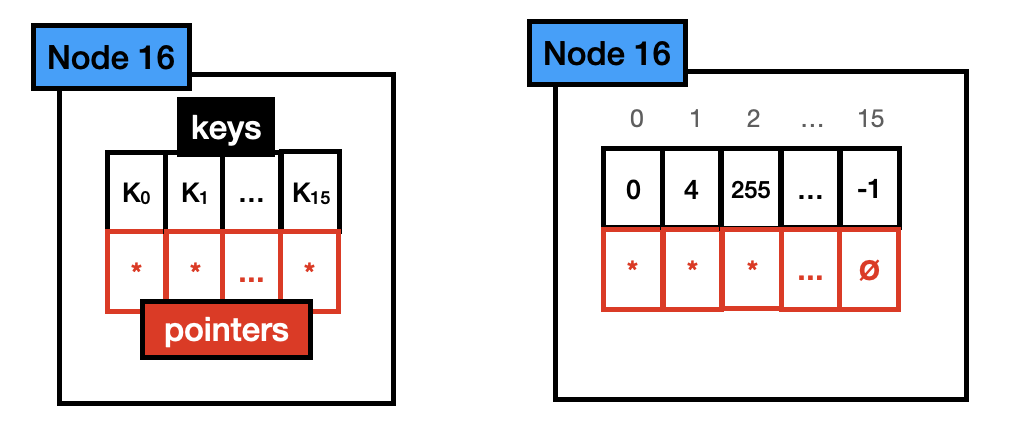
节点 48:节点 48 最多容纳 48 个不同的键。当此节点中存在键时,表示该键的单字节数组位置将保存一个索引到指针数组的索引,该索引指向该键的子节点。总大小为 640 字节 (256*1 + 48*8)。请注意,指针数组和键数组不再对齐。键数组指向指针数组中存储该键的指针的位置(例如,键数组中的键 255 设置为 2,因为指针数组的位置 2 指向与该键相关的子节点)。
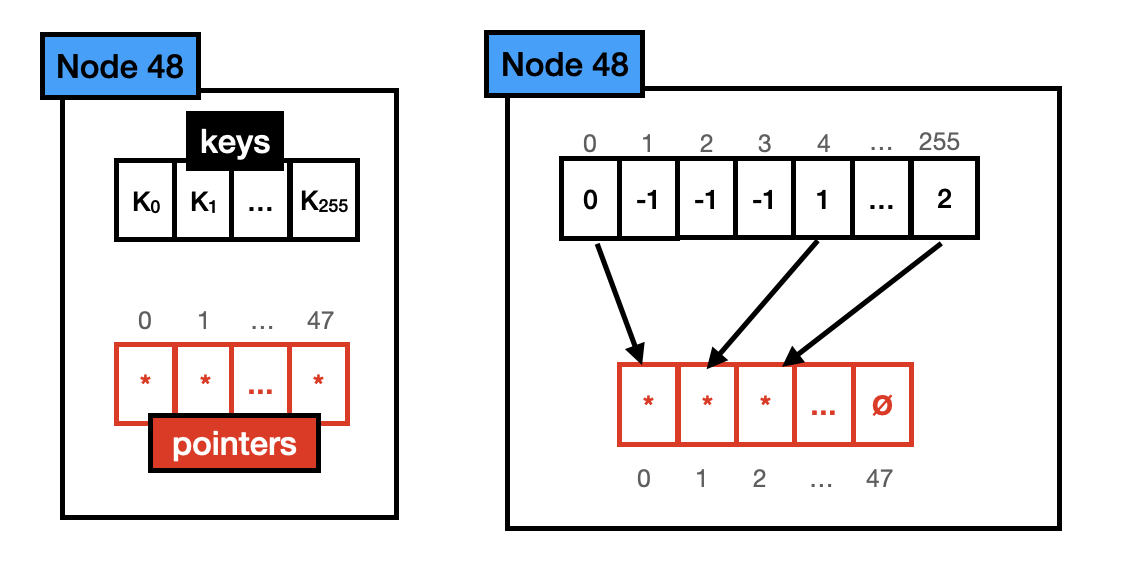
节点 256:节点 256 最多容纳 256 个不同的键,因此是分布中的所有可能值。它只有一个指针向量,如果指针已设置,则键存在,并且它指向其子节点。总大小为 2048 字节 (256 个指针 * 8 字节)。
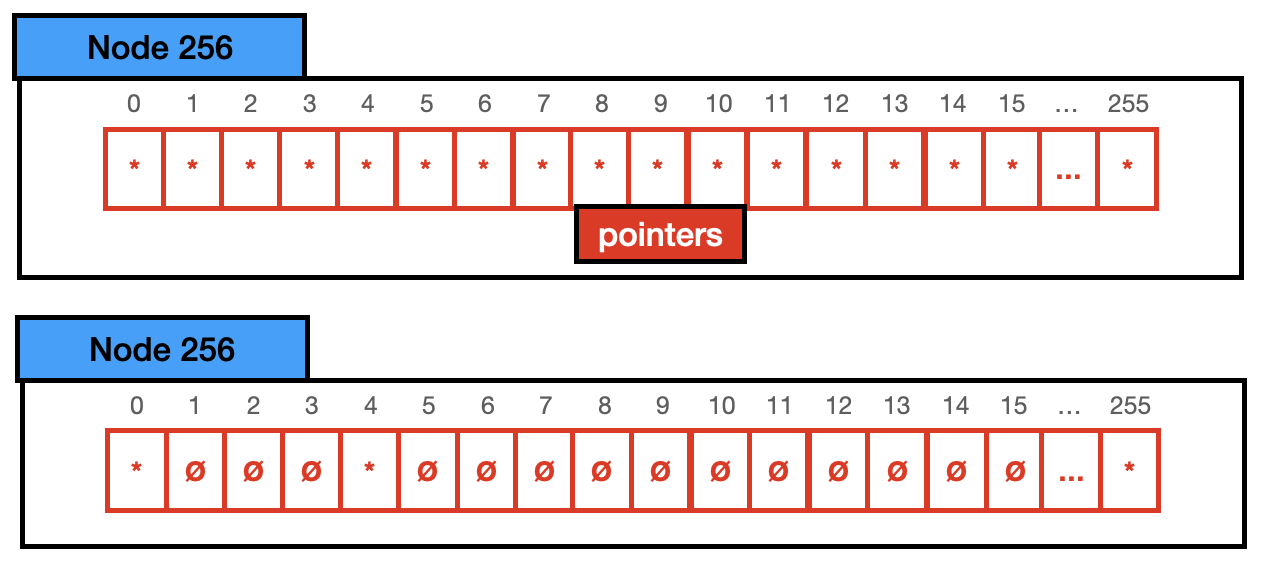
对于上一节中的示例,我们可以使用 Node 4 而不是 Node 256 来存储键,因为我们只有 3 个键。因此它看起来像下面这样
DuckDB 中的 ART
在考虑要在 DuckDB 中实现哪种索引结构时,我们想要一种结构,该结构可用于保持 PK/FK/Unique 约束,同时还能够加速范围查询和连接。数据库系统通常实现 哈希表 用于约束检查,并实现 BP 树 用于范围查询。但是,我们从 ART 索引中看到了通过使用一个数据结构来解决两个用例的机会,从而减少代码的复杂性。我们利用 ART 索引提供的主要特征是
- 紧凑的结构。由于 ART 内部节点相当小,因此可以放入 CPU 缓存中,成为比 BP 树更具缓存意识的结构。
- 快速点查询。ART 点查询的最坏情况是 O(k),这对于约束检查来说足够快。
- 插入时没有显着回归。许多哈希表变体必须在达到一定大小时重建。实际上,一次插入可能会导致时间显着回归,并且查询突然花费的数量级更多的时间才能完成,而用户没有任何明显的原因。在 ART 中,插入可能会导致节点增长(例如,节点 4 可能会增长到节点 16),但这些成本不高。
- 运行范围查询的能力。虽然 ART 运行范围查询的速度不如 BP 树,因为它必须执行树遍历,而 BP 树可以按顺序扫描叶节点,但它仍然优于哈希表,因为可以完成这些类型的查询(有些人可能会争辩说您可以使用哈希表进行范围查询,但算了吧)。这使我们能够有效地使用 ART 进行高选择性范围查询和索引连接。
- 可维护性。使用一种结构进行约束检查和范围查询,而不是两种结构,可以提高代码效率和可维护性。
它用于什么?
如前所述,ART 索引主要用于 DuckDB 的三个方面。
-
数据约束。主键、外键和唯一约束都由 ART 索引维护。当在具有约束的元组中插入数据时,这实际上会尝试在 ART 索引中执行插入,如果元组已经存在,则会失败。
CREATE TABLE integers (i INTEGER PRIMARY KEY); -- Insert unique values into ART INSERT INTO integers VALUES (3), (2); -- Insert conflicting value in ART will fail INSERT INTO integers VALUES (3); CREATE TABLE fk_integers (j INTEGER, FOREIGN KEY (j) REFERENCES integers(i)); -- This insert works normally INSERT INTO fk_integers VALUES (2), (3); -- This fails after checking the ART in integers INSERT INTO fk_integers VALUES (4); -
范围查询。索引列上的高选择性范围查询也将使用底层的 ART 索引。
CREATE TABLE integers (i INTEGER PRIMARY KEY); -- Insert unique values into ART INSERT INTO integers VALUES (3), (2), (1), (8) , (10); -- Range queries (if highly selective) will also use the ART index SELECT * FROM integers WHERE i >= 8; -
连接。匹配数量少的连接也将利用现有的 ART 索引。
-- Optionally you can always force index joins with the following pragma PRAGMA force_index_join; CREATE TABLE t1 (i INTEGER PRIMARY KEY); CREATE TABLE t2 (i INTEGER PRIMARY KEY); -- Insert unique values into ART INSERT INTO t1 VALUES (3), (2), (1), (8), (10); INSERT INTO t2 VALUES (3), (2), (1), (8), (10); -- Joins will also use the ART index SELECT * FROM t1 INNER JOIN t2 ON (t1.i = t2.i); -
表达式上的索引。ART 索引也可用于快速查找表达式。
CREATE TABLE integers (i INTEGER, j INTEGER); INSERT INTO integers VALUES (1, 1), (2, 2), (3, 3); -- Creates index over the i + j expression CREATE INDEX i_index ON integers USING ART((i + j)); -- Uses ART index point query SELECT i FROM integers WHERE i + j = 2;
ART 存储
存储 ART 索引时有两个主要约束
- 索引必须以允许延迟加载的顺序存储。否则,我们将不得不完全加载索引,包括对于该会话中将要执行的查询可能不需要的节点。
- 它不能增加节点大小。否则,我们将降低 ART 索引的缓存意识有效性。
后序遍历
为了允许延迟加载,我们必须存储一个节点的所有子节点,收集有关每个子节点的存储位置的信息,然后,在存储实际节点时,我们存储其每个子节点的磁盘信息。为了执行这种类型的操作,我们进行后序遍历。
后序遍历如下图所示。红色圆圈代表节点的存储顺序。如果我们从根节点开始(即,存储顺序为 10 的节点 4),我们必须首先存储两个子节点(即,存储顺序为 8 的节点 16 和存储顺序为 9 的叶节点)。这对于每个子节点递归进行。
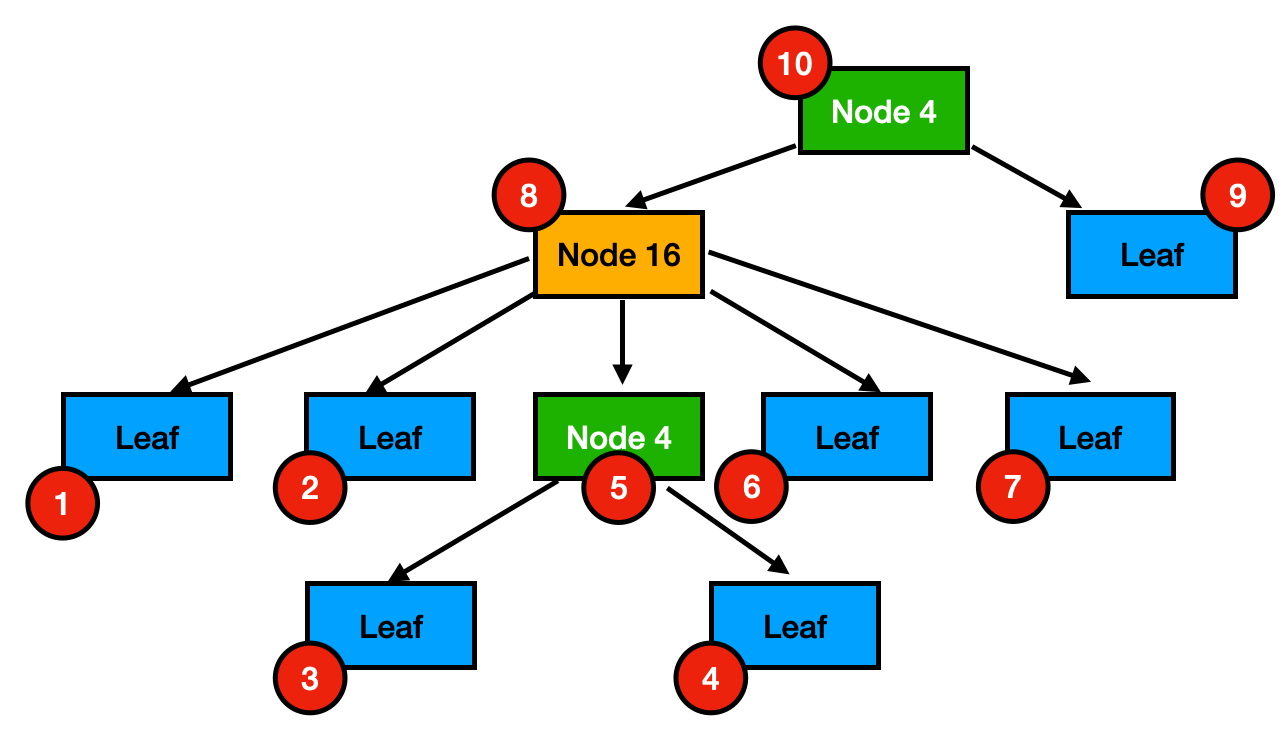
下图显示了 DuckDB 块格式的实际表示形式。在 DuckDB 中,数据存储在 256 kB 的连续块中,其中一些块保留用于元数据,一些块用于实际数据。每个块都由一个 id 表示。为了允许在块内导航,它们按字节偏移量进行分区,因此每个块包含 256,000 个不同的偏移量
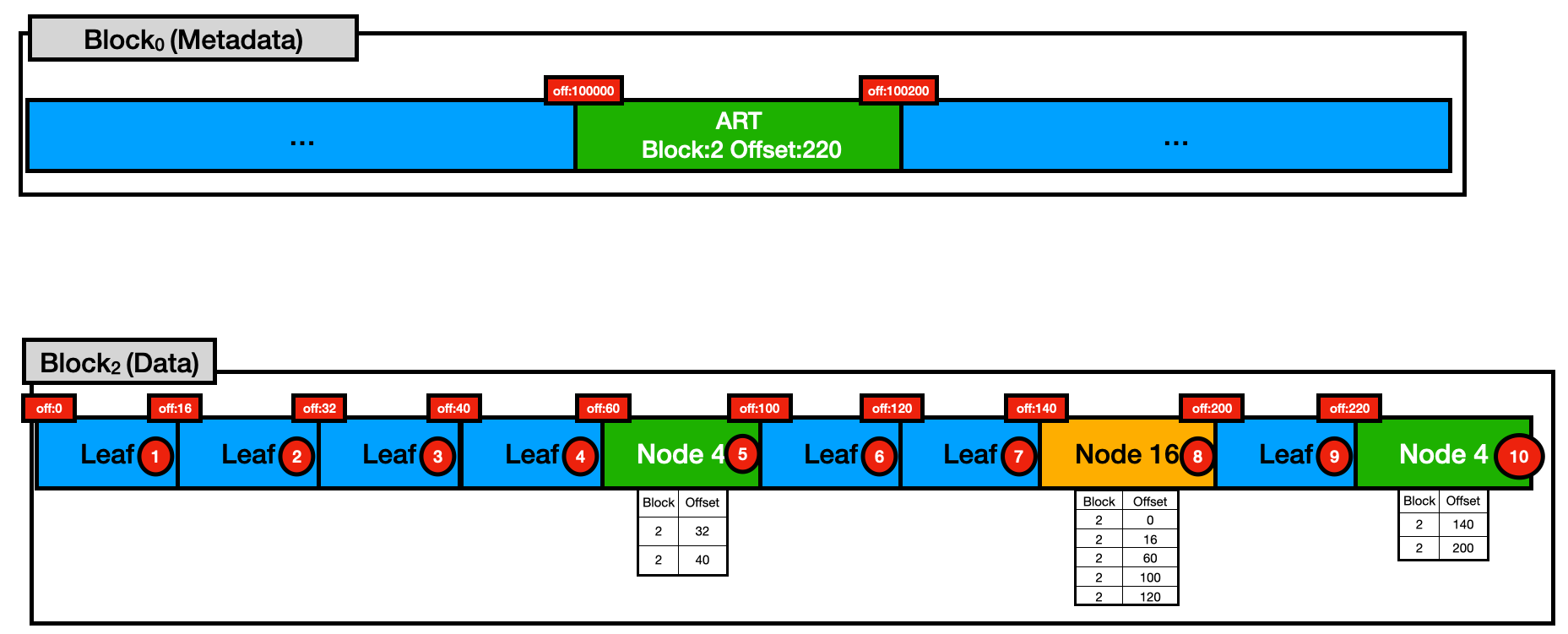
在此示例中,我们有 块 0,它存储了一些我们的数据库元数据。特别是,在偏移量 100,000 和 100,200 之间,我们存储与一个 ART 索引相关的信息。这将存储有关索引的信息(例如,名称、约束、表达式)及其根节点的 <块,偏移量> 位置。
例如,假设我们正在查找一个键,该键的 row_ids 存储在存储顺序为 1 的叶节点中。我们将首先加载 <块:2, 偏移量:220> 上的 Art 根节点,通过检查存储在该节点中的键,然后我们会看到我们必须加载 <块:2, 偏移量:140> 上的节点 16,然后最后加载 <块:0, 偏移量:0> 上的叶节点。这意味着对于此查找,仅将这 3 个节点加载到内存中。随后对这些节点的访问将只需要内存访问,而访问不同的节点(例如,叶节点存储顺序 2)仍然会导致磁盘访问。
实现此(反)序列化过程的一个主要问题是,现在我们不仅需要保留有关指针内存地址的信息,还需要保留它们是否已在内存中,如果不是,它们的存储位置 <块,偏移量> 是什么。
如果我们将块 ID 和偏移量存储在新变量中,它将极大地增加 ART 节点的大小,从而降低其作为缓存感知数据结构的有效性。
以节点 256 为例。保存 256 个指针的成本为 2048 字节(256 个指针 * 8 字节)。假设我们决定在一个新数组中存储块信息,如下所示
struct BlockPointer {
uint32_t block_id;
uint32_t offset;
}
class Node256 : public Node {
// Pointers to the child nodes
Node* children[256];
BlockPointer block_info[256];
}
节点 256 将增加 2048 字节 (256 * (4+4)),从而使其当前大小加倍至 4096 字节。
指针替换
为了避免 ART 节点大小的增加,我们决定实现 可替换指针,并使用它们代替常规指针。
我们的想法是,我们不需要指针中的所有 64 位(即,48 位为您提供 256 TB 的地址空间,支持任何当前的架构,请参阅 Stack Overflow 上的相关讨论和 “64 位计算”维基百科页面)来指向内存地址。因此,我们可以使用最高有效位作为标志(即,替换标志)。如果设置了替换标志,则我们的可替换指针中的值是节点的内存地址。否则,该变量存储节点存储位置的块信息。在后一种情况下,我们使用以下 31 位来存储块 ID,其余 32 位存储偏移量。
在下图中,您可以看到 DuckDB 可替换指针的可视化表示。
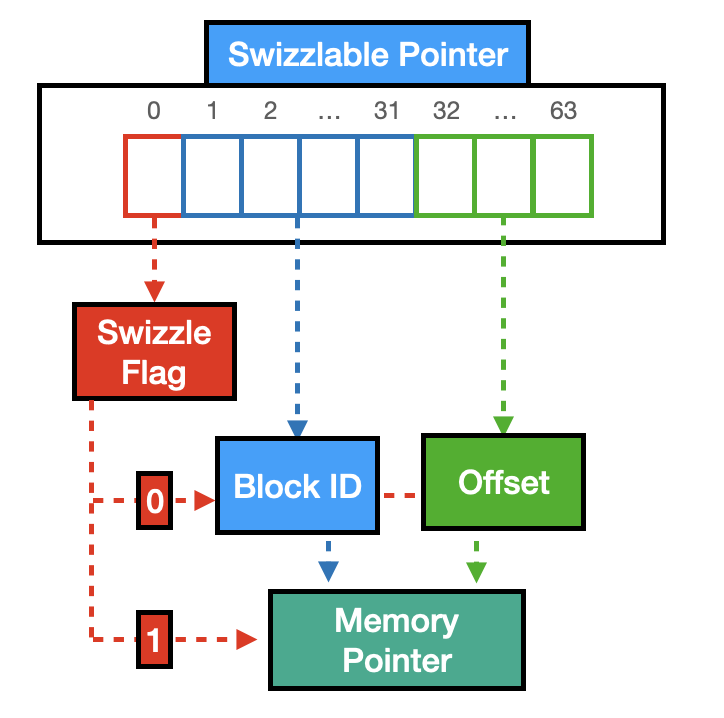
基准测试
为了评估当前存储实现的优点和缺点,我们运行了一个基准测试(可在以下 Colab 链接 中获得),我们在其中创建一个包含 50,000,000 个整数元素的表,并在其顶部设置主键约束。
con = duckdb.connect("vault.db")
con.execute("CREATE TABLE integers (x INTEGER PRIMARY KEY)")
con.execute("INSERT INTO integers SELECT * FROM range(50000000)")
我们在两个不同的 DuckDB 版本上运行此基准测试,一个版本不存储索引(即,v0.4.0),这意味着它始终在内存中,并在数据库重新启动时完全重建,另一个版本存储索引(即,最新版本),使用先前描述的延迟加载技术。
存储时间
我们首先测量序列化索引的额外成本。
cur_time = time.time()
con.close()
print("Storage time: " + str(time.time() - cur_time))
存储时间
| 名称 | 时间 (秒) |
|---|---|
| 重建 | 8.99 |
| 存储 | 18.97 |
我们可以看到,存储索引比不存储索引贵 2 倍。原因是我们的表由一列,其中包含 50,000,000 个 int32_t 值。但是,在存储 ART 时,我们还在叶节点中存储 50,000,000 个 int64_t 值,用于它们各自的 row_ids。元素的增加是额外存储成本的主要原因。
加载时间
我们现在测量重启数据库的加载时间。
cur_time = time.time()
con = duckdb.connect("vault.db")
print("Load time: " + str(time.time() - cur_time))
| 名称 | 时间 (秒) |
|---|---|
| 重建 | 7.75 |
| 存储 | 0.06 |
在这里,我们可以看到加载数据库的时间相差两个数量级。此差异主要是由于在加载期间完全重建 ART 索引。相比之下,在 Storage 版本中,此时仅加载有关 ART 索引的元数据信息。
查询时间(冷)
我们现在测量运行索引上的点查询的冷查询时间(即,数据库刚刚重新启动,这意味着在 Storage 版本中,索引尚未存在于内存中)。我们运行 5000 个点查询,这些点查询在我们的分布中的 10000 个元素上等距分布。我们使用此值来始终强制点查询加载大量未使用的节点。
times = []
for i in range (0, 50000000, 10000):
cur_time = time.time()
con.execute("SELECT x FROM integers WHERE x = " + str(i))
times.append(time.time() - cur_time)
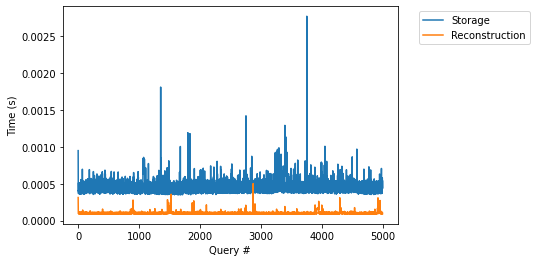
一般来说,在持久存储格式中,每个查询的成本高出 3 倍。这主要是由于两个主要原因:1)创建节点。在存储版本中,我们确实延迟创建节点,这意味着对于每个节点,必须分配所有参数,并加载键和前缀之类的值。2)块锁定。在每个节点,我们必须锁定和解锁存储它们的块。
查询时间(热)
在此实验中,我们执行与上一节中相同的查询。
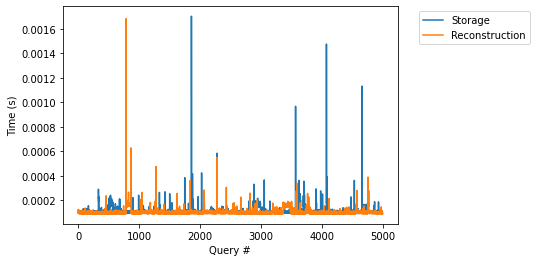
两个版本中的时间是可比较的,因为存储版本中的所有节点都已在内存中设置。总之,当存储的索引处于活动使用状态时,它们会呈现与完全在内存中的索引相似的性能。
未来工作
ART 索引存储一直是 DuckDB 中一个长期存在的问题,许多用户声称它是一个缺失的功能,阻碍了他们使用 DuckDB。虽然现在可以存储和延迟加载 ART 索引,但我们仍然可以采取许多未来的路径来使 ART 索引更高效。在这里,我列出了我认为最重要的后续步骤
- 缓存锁定的块。在我们当前的实现中,块会不断地锁定和解锁,即使块可以存储多个节点,并且很可能通过查找连续重用。智能地缓存它们将为触发节点加载的查询带来巨大的节省。
- 批量加载。我们的 ART 索引目前不支持批量加载。这意味着在列上创建索引时,由于元素将逐个插入,因此节点将不断调整大小。如果我们批量加载数据,我们可以准确地知道必须为该数据集创建哪些节点,从而避免了这些频繁的调整大小。
- 批量插入。当执行批量插入时,会发生与批量加载类似的问题。可能的解决方案是使用批量加载创建一个新的 ART 索引,然后将其与现有的 Art 索引合并
- 向量化查找/插入。DuckDB 使用向量化执行引擎。但是,我们的 ART 查找和插入仍然遵循一次一个元组的模型。
- 可更新的索引存储。在我们当前的实现中,ART 索引从磁盘完全失效并再次存储。这导致后续存储的存储时间不必要地增加。直接将节点更新到磁盘而不是完全重写索引可以极大地降低未来的存储成本。换句话说,索引会在每个检查点始终完全存储。
- 组合指针/行 ID 叶节点。我们当前的叶节点格式允许存储在多个元组上重复的值。但是,由于 ART 索引通常用于保持唯一键约束(例如,主键),并且唯一的
row_id适合相同的指针大小空间,因此可以通过使用子指针指向实际的row_id而不是创建一个仅存储一个row_id的实际叶节点来节省大量空间。
路线图
很难做出预测,尤其是关于未来的
– Yogi Berra
Art 索引是 DuckDB 中约束强制和保持访问速度的核心部分。如前一节所述,我们可以在 ART 好东西包中采用许多不同的路径,这些路径对于完全不同的用例具有优势。

为了更好地了解如何使用我们的索引,如果您能回答我们的一位理学硕士学生创建的以下调查问卷,将会非常有帮助。



